Estimated Reading Time: 8 minutes

Have You ever asked GPT the same question twice and gotten different answers? Even when you set the temperature to zero (which should make responses deterministic), variations still occur. This seemingly simple observation reveals a fascinating technical challenge that affects every large language model currently in production.

Let me walk you through what I have learnt so far. When you interact with a language model, you might think of it as a mathematical function, where the same input should give the same output, right? Unfortunately, the reality is more complicated. Even when we remove all randomness from the sampling process (by setting the temperature to 0), the models still produce different results.

Here’s a simple experiment you can conceptually understand,

# Conceptual example - what we expect
prompt = "Tell me about the AI"
response1 = llm.generate(prompt, temperature=0)
response2 = llm.generate(prompt, temperature=0)

# We expect: response1 == response2
# Reality: response1 != response2 (often different!)

This inconsistency isn’t just an academic curiosity, it has real implications for reproducible research, debugging, advanced training techniques and real world enterprise applications.

The most common explanation you’ll hear goes like this, “GPUs process things in parallel, and floating-point math isn’t perfectly associative, so the order of operations can vary based on which thread finishes first.” This explanation sounds reasonable, but it’s actually bit misleading!

Let me show you why with a simple test:

import torch

A = torch.randn(2048, 2048, device='cuda', dtype=torch.bfloat16)
B = torch.randn(2048, 2048, device='cuda', dtype=torch.bfloat16)

first_result = torch.mm(A, B)
for _ in range(1000):
    result = torch.mm(A, B)
    # Check that differences are effectively zero
    assert (result - first_result).abs().max().item() == 0

For torch.mm(A, B) the internal operations above happen in the same order each time. Think about what happens when we multiply two 2048×2048 matrices. To compute just one element of the output matrix, code looks like the following

python# Computing output[i,j] requires:
result = 0
for k in range(2048):
    result += A[i,k] * B[k,j]  # 2048 multiplications and additions

So for the full matrix multiplication, we’re doing about ~billion operations here! The GPU has to decide how to organize all of this work. The GPU kernel (the actual program running on the GPU) makes decisions like:

• How to split the work across cores: “I’ll give rows 0-127 to core 1, rows 128-255 to core 2, etc.”
• How to tile the computation: “Each core will process 128×128 blocks at a time”
• How to accumulate partial sums: “I’ll add up groups of 32 numbers, then combine those results”

So when we call torch.mm(A, B) with the same inputs repeatedly, the GPU uses the exact same recipe each time. It splits the work the same way, uses the same tile sizes, and accumulates the partial results in the same order. That’s why we get bitwise identical results.

Despite using floating-point numbers and employing massive parallelism on the GPU, we consistently obtain identical results. So the concurrency and floating maths hypothesis doesn’t fully explain what’s happening.

What if we change the matrix sizes slightly?

python# These might use different internal strategies!
C1 = torch.mm(A[:1024, :], B)  # 1024×2048 matrix multiply
C2 = torch.mm(A[:2048, :], B)  # 2048×2048 matrix multiply

The kernel might think: “Oh, this is a smaller matrix, I’ll use a different tile size for better efficiency” or “This is small enough that I don’t need to split across as many cores.” These different strategies can lead to different accumulation orders and thus different floating-point rounding. This is exactly what happens in LLM inference with varying batch sizes. When your request gets batched with 10 other requests versus 100 other requests, the matrix multiplications inside the model have different dimensions, triggering different computation strategies.

So Yes, when we repeatedly call torch.mm(A, B) with identical A and B, the multiplications and additions happen in exactly the same order each time. The GPU kernel is deterministic for fixed inputs.

Lets now discuss why non deterministic? or Why deterministic?

Imagine you’re using an LLM API. You send your request: “Explain Who is Manpreet.” But you’re not alone other people are sending requests at the exact same moment.

Here’s what the server is seeing

python# At 10:00:00.000 AM, the server receives:
user_requests = [
    {"user": "Mehr", "prompt": "Explain Who is Manpreet"},
    {"user": "Reni", "prompt": "Write a poem about cats"},
    {"user": "Sim", "prompt": "Translate this to French: Hello"},
]
# Batch size = 3

The server doesn’t process these one by one that would be inefficient. Instead, it combines them into a batch and processes them together through the neural network.

Now, here’s where things get interesting. A millisecond later, the load might be different:

python# At 10:00:00.001 AM, the server receives:
user_requests = [
    {"user": "Mehr", "prompt": "Explain Who is Manpreet"},  # Same request!
    {"user": "Reni", "prompt": "Debug my Python code"},
    {"user": "Sim", "prompt": "Recipe for chocolate cake"},
    {"user": "Mandy", "prompt": "Summary of World War 2"},
    # ... 20 more users ...
]
# Batch size = 24

The identical request (“Explain Who is Manpreet”) is now being processed alongside 23 other requests instead of just 2. This changes the dimensions of every matrix operation inside the neural network.

Tip: Just so that you keep you memory refreshed, during inference the attention scores are computed because they depend on the live input. They are not stored. Only projection weights are.

Something like this is happening inside the model,

# Simplified view of what happens inside one attention layer:

# Scenario 1: Your request with 2 others (batch_size = 3)
# If each prompt becomes ~50 tokens after embedding:
attention_matrix_1 = compute_attention(
    shape=[3, num_heads, 50, hidden_dim]  # 3 requests
)

# Scenario 2: Your request with 23 others (batch_size = 24)
attention_matrix_2 = compute_attention(
    shape=[24, num_heads, 50, hidden_dim]  # 24 requests
)

The GPU kernel that computes attention looks at these dimensions and makes optimization decisions like different stratergies. Each strategy involves adding floating-point numbers in a different order. Due to floating point arithmetic properties (assosiative), different orders give slightly different results.

# Imagine computing attention scores that need to sum three values:
values = [1e-8, 1e20, -1e20]

# Strategy A (small batch): Sum left to right
result_A = (1e-8 + 1e20) + (-1e20)  
# The 1e-8 gets lost when added to 1e20
# Result: 0.0

# Strategy B (large batch): Sum differently due to parallelization
result_B = 1e-8 + (1e20 + (-1e20))
# The large numbers cancel first
# Result: 1e-8

print(f"Strategy A result: {result_A}")  # 0.0
print(f"Strategy B result: {result_B}")  # 1e-8

These tiny differences accumulate through the network’s many layers. By the time the model generates tokens, these small numerical differences can cause it to select different words. This is why even with temperature=0 (which removes sampling randomness), you still get variations. The model’s internal computations literally change based on how many other people are using the service at that exact moment. Your request is deterministic given the entire batch, but since you can’t control or know who else is making requests, from your perspective it appears nondeterministic.

Question: If I always maintain the same number of requests, i should get deterministic results?

When you fix the batch size, you’re essentially forcing the GPU to always use the same computation strategy. Every matrix multiplication inside the model always has the same dimensions. The attention computation always splits work across cores the same way. The reduction operations always follow the same pattern. And therefore… you get bitwise identical results for identical inputs.

# Experiment: Same prompt, different batch configurations

prompt = "Explain gravity in one sentence"

# Configuration 1: Always batch size 4
for trial in range(10):
    batch = [prompt, "filler1", "filler2", "filler3"]  # Always 4 requests
    output = model.generate(batch)[0]  # Get our prompt's output
    print(f"Trial {trial}: {output}")

# Results:
# Trial 0: "Gravity is a fundamental force that attracts objects with mass toward each other."
# Trial 1: "Gravity is a fundamental force that attracts objects with mass toward each other."
# Trial 2: "Gravity is a fundamental force that attracts objects with mass toward each other."
# ... (all identical!)

# Configuration 2: Varying batch sizes
for trial in range(10):
    import random
    batch_size = random.randint(1, 32)
    batch = [prompt] + ["filler"] * (batch_size - 1)
    output = model.generate(batch)[0]
    print(f"Trial {trial} (batch_size={batch_size}): {output}")

# Results:
# Trial 0 (batch_size=3): "Gravity is a fundamental force that attracts objects with mass toward each other."
# Trial 1 (batch_size=17): "Gravity is the fundamental force that pulls objects with mass toward one another."
# Trial 2 (batch_size=7): "Gravity is a force that attracts objects with mass toward each other."
# ... (variations in wording!)

The nondeterminism isn’t inherent to the neural network computation itself it’s a consequence of dynamic batching for efficiency. Let’s just always use the same batch size! But that is always wasted computation and variable load handling. If you always maintain the same number of input requests (the batch size), then for any given input query, the model will produce identical token probability distributions every single time. Let me break down precisely what this means, because it’s actually quite remarkable when you think about it. The model computes probabilities for every possible next token in its vocabulary (often around 50,000 tokens). These probabilities are computed through a series of matrix operations, layer normalizations, and attention mechanisms. When the batch size is fixed, all these operations happen identically, producing the exact same probability distribution.

Tip: attention scores will not change if you run the exact same query 100 times with deterministic inference settings.

The critical insight is that with a fixed batch size, those logits (the raw scores before probability conversion) are bitwise identical every time.

# With fixed batch size, this chain of computations is identical every time:
input_query = "The capital of France is"
batch_size = 8  # Always exactly 8 requests

# Step 1: Embedding and attention computations
hidden_states = model.embed(input_query)  # Same result every time
for layer in model.layers:
    hidden_states = layer(hidden_states, batch_size=8)  # Same operations
    
# Step 2: Final layer produces logits (pre-probability scores)
logits = model.final_layer(hidden_states)
# With batch_size=8, these logits are IDENTICAL every run
# Example: logits["Paris"] = 15.2341, logits["London"] = 8.7632, etc.

# Step 3: Convert to probabilities
probabilities = softmax(logits / temperature)
# If temperature=0, we pick the highest logit (deterministic)
# If temperature>0, we sample from these probabilities (random)

Look at this output, even with identical probabilities, if the temperature is greater than 0, you might still see different output text because the model samples from these probabilities:

# Run 1 (batch_size = 8):
# P("Paris") = 0.7823
# P("London") = 0.0021
# P("Berlin") = 0.0018
# ... (exact values for all 50,000 tokens)

# Run 2 (batch_size = 8, same input):
# P("Paris") = 0.7823  # Exactly the same!
# P("London") = 0.0021  # Exactly the same!
# P("Berlin") = 0.0018  # Exactly the same!

# Run 3 (batch_size = 16, different batch size):
# P("Paris") = 0.7819  # Slightly different!
# P("London") = 0.0023  # Slightly different!
# P("Berlin") = 0.0017  # Slightly different!

My Mind Map

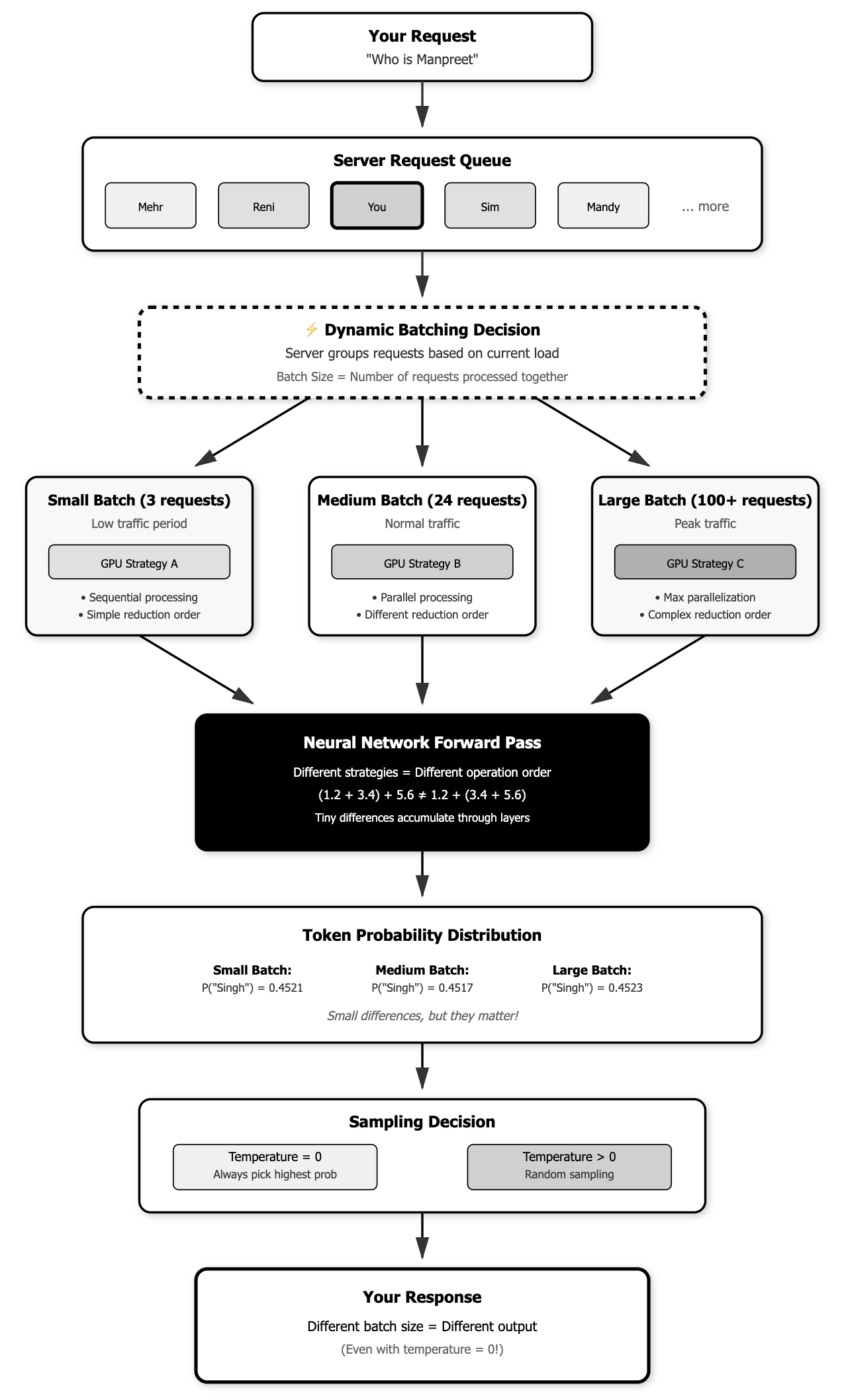
With the input “who is manpreet” should always produce the same probabilities, The probabilities themselves are changing based on how many other requests are being processed simultaneously. This happens because the forward pass computations are done slightly differently for different batch sizes.

# The reality of current LLM systems:

# Monday morning (few users online, batch_size = 3)
input = "who is manpreet"
probabilities_monday = model.forward(input, batch_size=3)
# P("Singh") = 0.4521
# P("Kaur") = 0.2103
# P("?") = 0.0876

# Monday afternoon (many users online, batch_size = 50)  
input = "who is manpreet"  # Exact same input!
probabilities_afternoon = model.forward(input, batch_size=50)
# P("Singh") = 0.4517  # Different!
# P("Kaur") = 0.2107   # Different!
# P("?") = 0.0874      # Different!

• Same batch size → Same probabilities → With temperature=0, same text output
• Different batch size → Different probabilities → Different text output (even with temperature=0)
• Temperature > 0 adds another layer of randomness on top of the probability variations

Tip: In LLM terminology, hallucination refers to when a model generates false or fabricated information that it presents. Nothing to do with being determinsitic or not.